Langsung ke konten utama

Menghitung Median Effective Dose/Concentration


Dalam penelitian farmakodinamik seringkali dibutuhkan analisis kurva dosis respon untuk menilai efektifitas suatu obat. Kurva dosis respon sendiri berbentuk sigmoid yang tidak mampu dianalisis menggunakan regresi linear sederhana. Untuk memodelkan kurva dosis respon sekaligus mencari nilai dosis atau konsentrasi tengah (ED50 atau IC50 atau EC50) akan lebih tepat apabila digunakan regresi non linear seperti logistik dan log-logistik.

Regresi Logistik
Bentuk umum dari regresi logistik dapat dilihat pada persamaan di bawah ini:
$$ f\left (x \right )=c+\frac{d-c}{\left (1+{e}^{\left (b\left (x-e \right ) \right )} \right ){}^{f}} $$
Dalam model tersebut, terdapat 5 buah konstanta yaitu b, c, d, e, dan f. Konstanta-konstanta tersebut tidak harus selalu disertakan dalam model. Dalam regresi logistik dikenal beberapa model yaitu L.3, L.4, dan L.5. Model L.3 menyertakan konstanta b, d, e; L.4  menyertakan b, c, d, e; dan L.5 menyertakan b, c, d, e, f dalam model regresinya.

Regresi Log-Logistik

Sebenarnya regresi log-logistik hampir sama dengan logistik hanya saja beberapa parameter dimodelkan dengan menggunakan bentuk logaritma. Berikut ini adalah bentuk umum regresi log-logistik:
$$ f\left (x \right )=c+\frac{d-c}{\left (1+{e}^{\left (b\left (log(x)-log(e) \right ) \right )} \right ){}^{f}} $$
Berikut ini adalah contoh hasil pemodelan kurva dosis respon dan perhitungan ED50 menggunakan regresi log-logistik (LL.3) di mana dosis obat diberikan dalam satuan konsentrasi molar.

b = -8,9190e-01; d = 9,6756e-01 , e = 9,8018e-08
ED50 = 9,8018e-08 ± 2,4735e-08 M


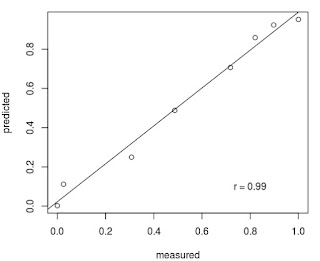
Untuk memastikan apakah hasil regresi log-logistik ini valid, dilakukan analisis kesesuaian fungsi secara visual predplot dan regresi linear antara nilai terprediksi dan nilai terukur.
Nilai hasil prediksi dan terukur cukup dekat dengan koefisien korelasi sebesar 0,99 sehingga dapat dikatakan bahwa persamaan tersebut adekuat untuk memodelkan hubungan antara dosis dan respon.

Probit

 Selain menggunakan regresi logistik atau log-logistik, dapat digunakan transformasi probit. Kurva dosis respon dianggap identik dengan kurva probabilitas kumulatif distribusi normal yang sama-sama berbentuk sigmoid. Respon (respon dibagi dengan respon maksimum) diubah menjadi probit (dapat melalui tabel probit atau dengan perintah NORM.S.INV pada excel atau qnorm dengan R) dan dosis diubah menjadi log10 dosis. Kemudian dilakukan operasi regresi linear antara log10 dosis (x) dengan respon probit (y) sehingga diperoleh persamaan regresi linear. Nilai dosis tengah (ED50 atau IC50) merupakan nilai di mana respon probit = 0. Dengan demikian log10 dosis 50 dapat dihitung dan selanjutnya dapat dikonversi menjadi dosis tengah.

 Berikut ini adalah contoh analisis probit dengan menggunakan data yang sama (respon 0 dan 1 dihilangkan karena tidak dapat dikonversi menjadi probit)

intercept = 8,16; slope = 1,20; r = 0,95; ED50 = 1,58e-7

 Hasil yang diperoleh sedikit berbeda antara probit dengan regresi log-logistik. Kalau begitu maka pertanyaannya adalah "manakah model yang dapat dipercaya?". Untuk menjawab ini maka kita lihat model mana yang terbaik. Kita dapat melihat signifikansi masing-masing koefisien regresi dengan menggunakan uji t.

Pertama-tama lihat signifikansi masing-masing variabel pada regresi log-logistik

nilai p <0,05 menunjukkan bahwa variabel signfikan. Nilai p untuk b, d, e <0,05 sehingga ketiga parameter regresi ini signifikan.

 Kedua lihat signfikansi slope pada regresi probit

nilai p untuk slope <0,05 sehingga dapat dikatakan bahwa slope pada regresi probit signifikan.

 Setelah memastikan bahwa semua koefisien signfikan, maka selanjutnya melihat nilai koefisien korelasinya. dalam model log-logistik nilai koefisien korelasi lebih besar sehingga dapat dikatakan bahwa derajat kesesuaian fungsi regresi log-logistik lebih kuat dibandingkan regresi probit. Dengan demikian dapat disimpulkan bahwa pemodelan menggunakan regresi log-logistik untuk kasus ini lebih baik dibandingkan dengan regresi linear dengan transformasi probit dan log-dosis. Sehingga perhitungan ED50 yang lebih tepat adalah 9,8018e-08 ± 2,4735e-08 M.
Referensi :

Ritz C, Baty F, Streibig JC, Gerhard D (2015) Dose-Response Analysis Using R. PLoS ONE 10(12): e0146021. https://doi.org/10.1371/journal.pone.0146021

 https://www.jacionline.org/article/0091-6749(88)90218-7/pdf



Label:

Komentar

Posting Komentar

Postingan populer dari blog ini

Memahami Potensial Aksi Sel Saraf : Depolarisasi, Hiperpolarisasi, Repolarisasi

Potensial Istirahat Membran Sinyal pada sel-sel saraf disampaikan melalui sinyal listrik. Sinyal listrik ini dapat terjadi karena ada perbedaan muatan di dalam dan di luar sel. Perbedaan muatan ini dapat diukur menggunakan voltmeter yang terhubung dengan elektroda pembanding dan mikroelektroda perekam (lihat Gambar 1). Pada keadaan istirahat kanal ion tertutup, ion yang tersebar di sepanjang membran dapat diprediksi dengan mudah. Konsentrasi Na +  diluar sel 10 kali lebih besar dari pada di dalam sel dan konsentrasi K +  di dalam sel lebih besar daripada di luar sel. Sitosol mengandung anion konsentrasi tinggi dalam bentuk ion fosfat dan protein yang terionisasi negatif. Pada keadaan ini (istirahat) muatan di dalam sel lebih negatif daripada di luar dan beda potensialnya sebesar -70 mV. Nilai ini disebut dengan potensial istirahat membran. Kebocoran kanal ion dapat terjadi yang memungkinkan ion Na +  masuk ke dalam sel atau ion K +  keluar dari sel, namun hal ini d...
Posting Komentar
Baca selengkapnya

Klasifikasi Reseptor

Reseptor dapat dibagi berdasarkan lokasi dan transduksi sinyal. Berdasarkan lokasinya, reseptor dapat dibagi menjadi reseptor transmembran dan reseptor inti. Jika ditinjau dari proses transduksi sinyal, maka dapat dibagi lagi menjadi  ionotropik &  metabotropik . Reseptor ionotropik, reseptor kanal ion atau yang terasosiasi dengan kanal ion, masih dapat dibagi lagi menjadi voltage-gated, ATP-gated, dan ligand-gated sedangkan reseptor ionotropik dapat dibagi menjadi reseptor terikat protein G (G s , G q , G i ) dan reseptor terikat enzim. 1. Reseptor Transmembran Reseptor transmembran terletak di membran sel dan mempunyai domain (daerah) ekstraseluler, membran, dan intraseluler [ 1 ]. Beberapa reseptor yang termasuk dalam golongan reseptor transmembran adalah reseptor insulin dan glucose transporter [2]  serta reseptor GABA A [3] . 2. Reseptor Inti Reseptor inti adalah reseptor yang terdapat di sitoplasma. Apabila terdapat ligan yang pengaktivas...
Posting Komentar
Baca selengkapnya

Transporter dalam dalam absorpsi obat : Kinetika Michaelis-Menten

Kinetika Michaelis-Menten (MM) sangat berguna untuk memahami proses disposisi obat dalam tubuh. Beberapa molekul obat bersifat polar sehingga tidak mampu berdifusi pasif untuk melewati membran sel. Transport molekul-molekul obat ini diperantarai oleh suatu molekul pembawa (umumnya protein) yang disebut dengan transporter. Pada hakekatnya, proses perpindahan/transport obat melalui molekul pembawa seperti reaksi enzimatis sehingga berlaku reaksi : $\ce{E + S <=>[k_1][k_3] ES ->[k_2][] E + P }$ Dalam konteks disposisi obat, tidak terjadi pembentukan produk. namun hanya perpindahan obat dari kompartemen apikal ke basolateral atau sebaliknya. sehingga persamaan reaksi lebih tepat apabila ditulis sebagai berikut: $\ce{E + S_{apikal} <=>[k_1][k_3] ES ->[k_2][] E + S_{basolateral} }$ atau $\ce{E + S_{basolateral} <=>[k_1][k_3] ES ->[k_2][] E + S_{apikal} }$ Dengan menggunakan pendekatan kinetika M-M maka dapat dituliskan kinetika perpindahan obat yaitu:...
Posting Komentar
Baca selengkapnya